物理信息神经网络PINN的实现及其应用场景
一. 物理信息神经网络 PINN 简介
物理信息神经网络(Physics-Informed Neural Networks, PINN)是一种结合深度学习和物理知识的神经网络模型。与传统数据驱动的神经网络模型相比,PINN 在训练过程中引入了物理约束,使得模型不仅能够学习数据中的模式,还能够满足物理定律,从而提高模型的泛化能力和预测精度。
PINN 的基本思想是将物理定律(如偏微分方程)作为先验知识嵌入到神经网络中,通过最小化数据损失和物理损失来训练模型。这样,PINN 不仅能够学习数据中的模式,还能够满足物理定律,从而提高模型的泛化能力和预测精度。
简单来讲,在 PINN 中的损失函数由两部分组成:
- 数据损失 \(L_{data}\)(Data Loss):衡量神经网络的预测值与实际数据之间的差异。
- 物理损失 \(L_{physics}\)(Physics Loss):衡量神经网络的预测值与物理定律之间的差异。
总损失函数表示为:
$$
L = L_{data} + L_{physics}
$$
二. PINN 的实现
下面以一个简单的波动方程(Wave Equation)为例,介绍 PINN 的实现方法。
2.1 问题描述
需要根据输入数据 \(x\)、 \(t\) 和输出数据 \(u(x,t)\),训练一个神经网络模型 \(ANN(x,t)\),使得模型能够根据输入数据预测输出数据,并且满足波动方程的约束条件。
在很多情况下,我们无法找到波动方程的具体解析解(比如 \(u(x,t) = \sin(2\pi(x-t))\)),但是我们可以通过物理信息神经网络来逼近波动方程的解析解,从而实现预测功能。
输入数据:\(x \in [-1, 1]\),\(t \in [0, 1]\)
输出数据:\(u(x,t)\)
(物理)约束条件:\(u(x,t)\) 满足波动方程 \(\frac{\partial u}{\partial t} + c\frac{\partial u}{\partial x} = 0\)
其中:
- \(u(x,t)\) 是波的位移
- \(c\) 是波速(这里取 \(c=1.0\))
- \(x\) 是空间坐标
- \(t\) 是时间坐标
2.2 虚拟数据生成
行波解是波动方程的解析解之一,这里我们假设 \(u(x,t)\) 满足行波解 \(u(x,t) = \sin(2\pi(x-t))\)。
其中:
- 波长 \(\lambda = 1\)
- 角频率 \(\omega = 2\pi c\)
- 相速度 \(c = 1.0\)
使用行波解生成一些虚拟数据,用于训练神经网络模型。
def generate_data(nx=100, nt=100, x_range=(-1, 1), t_range=(0, 1)):
x = np.linspace(x_range[0], x_range[1], nx)
t = np.linspace(t_range[0], t_range[1], nt)
X, T = np.meshgrid(x, t)
# 解析解
c = 1.0
u_exact = np.sin(2*np.pi*(X - c*T))
2.3 构建神经网络
网络结构:
- 输入层:2个节点 \((x,t)\)
- 隐藏层:3层,每层20个节点
- 输出层:1个节点 \(u(x,t)\)
- 激活函数:tanh
class Net(nn.Module):
def __init__(self, input_size=2, hidden_size=20, output_size=1):
super(Net, self).__init__()
self.fc1 = nn.Linear(input_size, hidden_size)
self.fc2 = nn.Linear(hidden_size, hidden_size)
self.fc3 = nn.Linear(hidden_size, hidden_size)
self.fc4 = nn.Linear(hidden_size, output_size)
2.4 构建损失函数
损失函数包含两部分:
物理约束损失:
$$
\mathcal{L}{PDE} = \frac{1}{N}\sum{i=1}^N |\mathcal{R}(x_i,t_i)|^2
$$
其中, 残差 \(\mathcal{R} = \frac{\partial u}{\partial t} + c\frac{\partial u}{\partial x}\)数据拟合损失:
$$
\mathcal{L}{data} = \frac{1}{N}\sum{i=1}^N |u_{pred}(x_i,t_i) - u_{exact}(x_i,t_i)|^2
$$
总损失函数:
$$
\mathcal{L} = \mathcal{L}{PDE} + \mathcal{L}{data}
$$
def loss_function(net, x, t, u_exact, c=1.0):
# 计算偏导数
u_t = torch.autograd.grad(u_pred, t, grad_outputs=torch.ones_like(u_pred),
create_graph=True)[0] # ∂u/∂x
u_x = torch.autograd.grad(u_pred, x, grad_outputs=torch.ones_like(u_pred),
create_graph=True)[0] # ∂u/∂t
# 计算PDE残差
residual = u_t + c * u_x # R = ∂u/∂t + c∂u/∂x
# 计算物理约束损失
L_PDE = torch.mean(residual**2) # (1/N)∑|R|²
# 计算数据拟合损失
L_data = torch.mean((u_pred - u_exact)**2) # (1/N)∑|u_pred - u_exact|²
# 总损失
loss = L_PDE + L_data
return loss
2.5 训练模型
训练过程使用Adam优化器,学习率为0.001,训练1500轮。
2.6 结果可视化
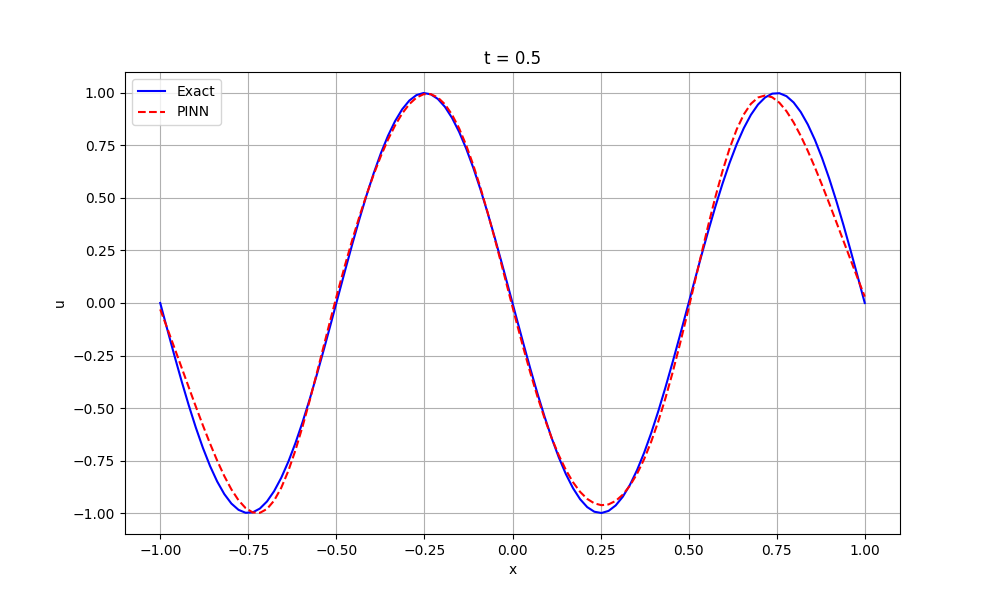
绘制t=0.5时刻的波形,比较:真实解(Exact)和预测解(PINN)之间的差异。
- 真实解:\(u_{exact} = \sin(2\pi(x - 0.5))\)
- 预测解:神经网络输出 \(ANN(x,t)\)
2.7 完整代码
import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np
import matplotlib.pyplot as plt
# 定义神经网络结构
class Net(nn.Module):
def __init__(self, input_size=2, hidden_size=20, output_size=1):
super(Net, self).__init__()
self.fc1 = nn.Linear(input_size, hidden_size)
self.fc2 = nn.Linear(hidden_size, hidden_size)
self.fc3 = nn.Linear(hidden_size, hidden_size)
self.fc4 = nn.Linear(hidden_size, output_size)
def forward(self, x):
x = torch.tanh(self.fc1(x))
x = torch.tanh(self.fc2(x))
x = torch.tanh(self.fc3(x))
x = self.fc4(x)
return x
# 生成训练数据
def generate_data(nx=100, nt=100, x_range=(-1, 1), t_range=(0, 1)):
x = np.linspace(x_range[0], x_range[1], nx)
t = np.linspace(t_range[0], t_range[1], nt)
X, T = np.meshgrid(x, t)
# 生成解析解(以简单的行波为例)
c = 1.0 # 波速
u_exact = np.sin(2*np.pi*(X - c*T))
return X.flatten(), T.flatten(), u_exact.flatten()
# 定义损失函数
def loss_function(net, x, t, u_exact, c=1.0):
# 将输入组合
inputs = torch.cat([x, t], dim=1)
# 前向传播得到预测值
u_pred = net(inputs)
# 计算偏导数
u_t = torch.autograd.grad(u_pred, t, grad_outputs=torch.ones_like(u_pred),
create_graph=True)[0]
u_x = torch.autograd.grad(u_pred, x, grad_outputs=torch.ones_like(u_pred),
create_graph=True)[0]
# 计算PDE残差
residual = u_t + c * u_x
# 计算物理约束损失
L_PDE = torch.mean(residual**2)
# 计算数据拟合损失
L_data = torch.mean((u_pred - u_exact)**2)
# 总损失
loss = L_PDE + L_data
return loss
# 主训练函数
def train_pinn():
# 设置设备
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
# 生成数据
X, T, U_exact = generate_data()
# 转换为PyTorch张量
x = torch.tensor(X, dtype=torch.float32).reshape(-1, 1).requires_grad_(True).to(device)
t = torch.tensor(T, dtype=torch.float32).reshape(-1, 1).requires_grad_(True).to(device)
u_exact = torch.tensor(U_exact, dtype=torch.float32).reshape(-1, 1).to(device)
# 初始化网络
net = Net().to(device)
# 定义优化器
optimizer = optim.Adam(net.parameters(), lr=0.001)
# 训练循环
epochs = 1500
for epoch in range(epochs):
optimizer.zero_grad()
# 计算损失
loss = loss_function(net, x, t, u_exact)
# 反向传播
loss.backward()
optimizer.step()
if (epoch + 1) % 100 == 0:
print(f'Epoch [{epoch+1}/{epochs}], Loss: {loss.item():.4f}')
return net, x, t, u_exact
# 可视化结果
def plot_results(net, x, t, u_exact):
with torch.no_grad():
# 创建新的规则网格点
x_plot = torch.linspace(-1, 1, 100, device=x.device).reshape(-1, 1)
t_plot = torch.full_like(x_plot, 0.5)
# 组合输入
inputs = torch.cat([x_plot, t_plot], dim=1)
# 计算预测值
u_pred = net(inputs)
# 计算对应的解析解
u_exact_plot = torch.sin(2*np.pi*(x_plot - t_plot))
# 绘图
plt.figure(figsize=(10, 6))
plt.plot(x_plot.cpu().numpy(), u_exact_plot.cpu().numpy(), 'b-', label='Exact')
plt.plot(x_plot.cpu().numpy(), u_pred.cpu().numpy(), 'r--', label='PINN')
plt.xlabel('x')
plt.ylabel('u')
plt.title('t = 0.5')
plt.legend()
plt.grid(True)
plt.show()
if __name__ == "__main__":
# 训练模型
net, x, t, u_exact = train_pinn()
# 绘制结果
plot_results(net, x, t, u_exact)
三. PINN 的应用场景
3.1 PINN 的优势
- PINN 可以通过损失函数强制模型满足物理约束,从而提高模型的物理合理性和可解释性。
- PINN 不需要大量的数据标注,只需要物理约束条件,因此可以大大减少数据标注的工作量。
3.2 PINN 的应用场景
PINN 的应用场景非常广泛,以下是一些典型的应用场景:
- 偏微分方程求解
- 多物理场耦合问题
- 复杂流体动力学问题
- 材料科学中的相场模拟
- 生物医学中的图像分析与处理

