信号复杂性的评估方法–各种熵
一、熵 (Entropy)
熵是衡量系统混乱程度的物理量,在热力学中,它代表了系统状态的无序程度。 在信息论中,熵被用来衡量信息的不确定性或信息量。 信息熵 (Information Entropy)是熵在信息论中的应用,由克劳德·香农提出,用于量化信息中包含的不确定性,很多情况下会把信息熵简称为熵。
这些熵值(相对熵、KL散度、交叉熵、模糊熵、样本熵、近似熵)都是用来表征信号序列复杂程度的无量纲指标,熵值越大代表信号复杂度越大。 信号复杂程度的表征在机械设备状态监测、故障诊断以及心率、血压信号检测中都十分有用;能够抵抗环境干扰的影响,广泛应用于特征提取的领域(如生物医学信号处理)当中。
对于一个离散随机变量 \(X\),其概率分布为 \(P(X)\),信息熵 \(H(X)\) 可以表示为\(X\)所有可能值的概率分布的函数,定义为:
\[H(X) = -\sum_{i} P(x_i) \log_b P(x_i)\]
其中,\(x_i\) 是 \(X\) 的第 \(i\) 个可能值,\(b\) 是对数的底,常见的 \(b\) 为 2 或自然底数 \(e\),分别对应比特和奈特作为信息的单位。
二、各种熵的定义
1、相对熵 (Relative Entropy) / KL散度 (Kullback-Leibler Divergence)
相对熵,也称为KL散度,是衡量两个概率分布P和Q差异的一种方法。它是非对称的,表示在同一个随机变量上用Q来近似P时损失的信息量。其公式表达了从P到Q的不精确度量。
对于两个离散概率分布 \(P(X)\) 和 \(Q(X)\) 上的随机变量 \(X\),KL散度定义为:
\[D_{KL}(P || Q) = \sum_{i} P(x_i) \log \frac{P(x_i)}{Q(x_i)}\]
这里,\(D_{KL}(P || Q)\) 不是对称的,即 \(D_{KL}(P || Q) \neq D_{KL}(Q || P)\)。
2、交叉熵 (Cross Entropy)
交叉熵是在分类问题中常用的一个概念,用于衡量两个概率分布之间的差异,特别是在机器学习的分类任务中,用于衡量实际输出与期望输出的差异。对于两个概率分布P和Q,交叉熵的计算包含了P分布的熵以及P分布相对于Q分布的KL散度。
对于两个离散概率分布 \(P(X)\) 和 \(Q(X)\),交叉熵 \(H(P, Q)\) 定义为:
\[H(P, Q) = -\sum_{i} P(x_i) \log Q(x_i)\]
交叉熵衡量的是,在真实分布为 \(P\) 的情况下,使用分布 \(Q\) 来编码事件所需的平均比特数。
3、近似熵 (Approximate Entropy,ApEn)
近似熵由 Steven M. Pincus 于 1991年从衡量信号序列复杂性的角度提出的[1]。 近似熵是衡量时间序列数据复杂度的一种方法,用于量化序列中新模式出现的概率,与样本熵相似但计算方式有所不同。近似熵较高意味着序列包含更多的不可预测性。
近似熵公式为:
\[ApEn(m,r)=\phi^{m}(r)-\phi^{m+1}(r)\]
参数选择:
- \(m\) 是时间序列中相比较的数据点的数量,通常选择m=2;
- \(r\) 是相似度容忍度,\(r\)在0.1和0.25 \(SD(x)\)(\(SD(x)\)是序列的标准差)之间, ApEn有比较合理的统计特性;
- \(N\) 是时间序列的总数据点数,一般输入点数要控制在100到5000这个范围内。
推导过程: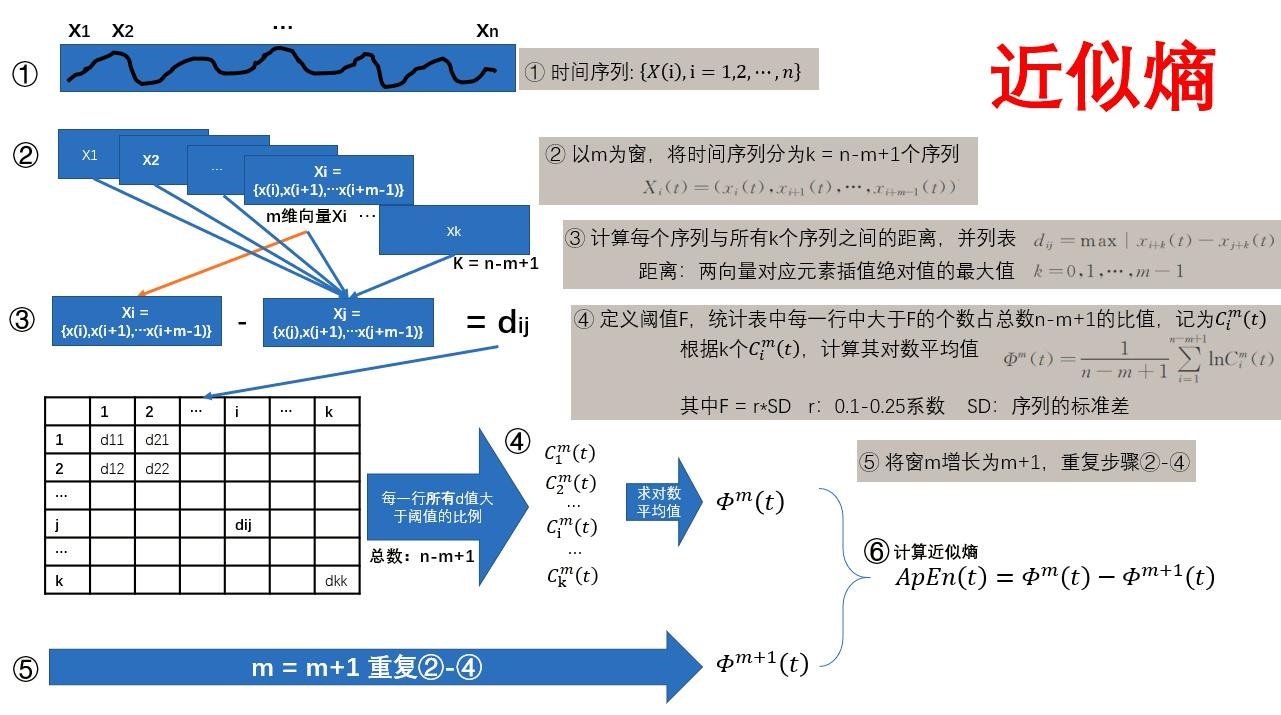
4、样本熵 (Sample Entropy,SamEn)
样本熵(Sample Entropy)是Richman等人提出的一种与近似熵不同的不计数自身匹配的统计量[3],是对近似熵算法的改进。 样本熵是一种用于量化时间序列复杂性的指标,与模糊熵类似,但在计算过程中不考虑序列中重复模式的自匹配,因此它对数据长度较不敏感,适用于分析较短的数据序列。
样本熵定义为:
$$
SampEn(m,r)=lnB^{m}(r)-lnA^{m}(r)
$$
参数选择:
- \( m \) 是时间序列中相比较的数据点的数量,通常m取1或者2,且取m=2更为多见;
- \( r \) 是相似度容忍度,通常\(r\)在0.1和0.25 \(SD(x)\)之间。
推导过程: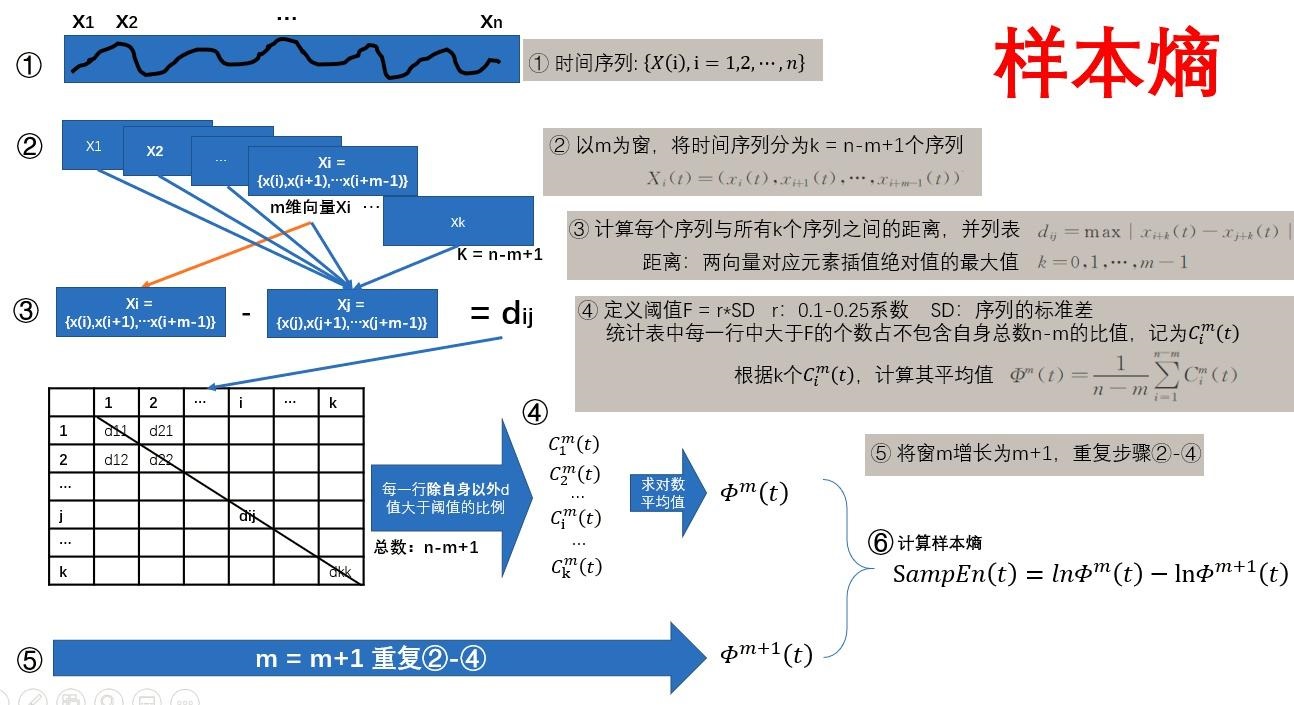
5、模糊熵 (Fuzzy Entropy, FuzzyEn)
模糊熵(Fuzzy Entropy)是陈伟婷[5]在2007年提出的,初衷是用于肌电型号处理中,不过其后在故障诊断、图像处理等领域也有着广泛的应用。
模糊熵表示为:
\[ FuzzyEn(m,n,r)=ln\phi^{m}(n,r)-ln\phi^{m+1}(n,r) \]
参数选择:
- \(m\) 是时间序列中相比较的数据点的数量,通常选择m=2;
- \(r\) 是模糊相似度阈值,\(r\)在0.1和0.25 \(SD(x)\)(\(SD(x)\)是序列的标准差)之间;
- \(n\) n 决定了相似容限边界的梯度,n 越大则梯度越大,n 在模糊熵向量间相似性的计算过程中起着权重的作用。为了捕获尽量多的细节信息,陈伟婷建议计算时取较小的整数值,如2或3等。
推导过程: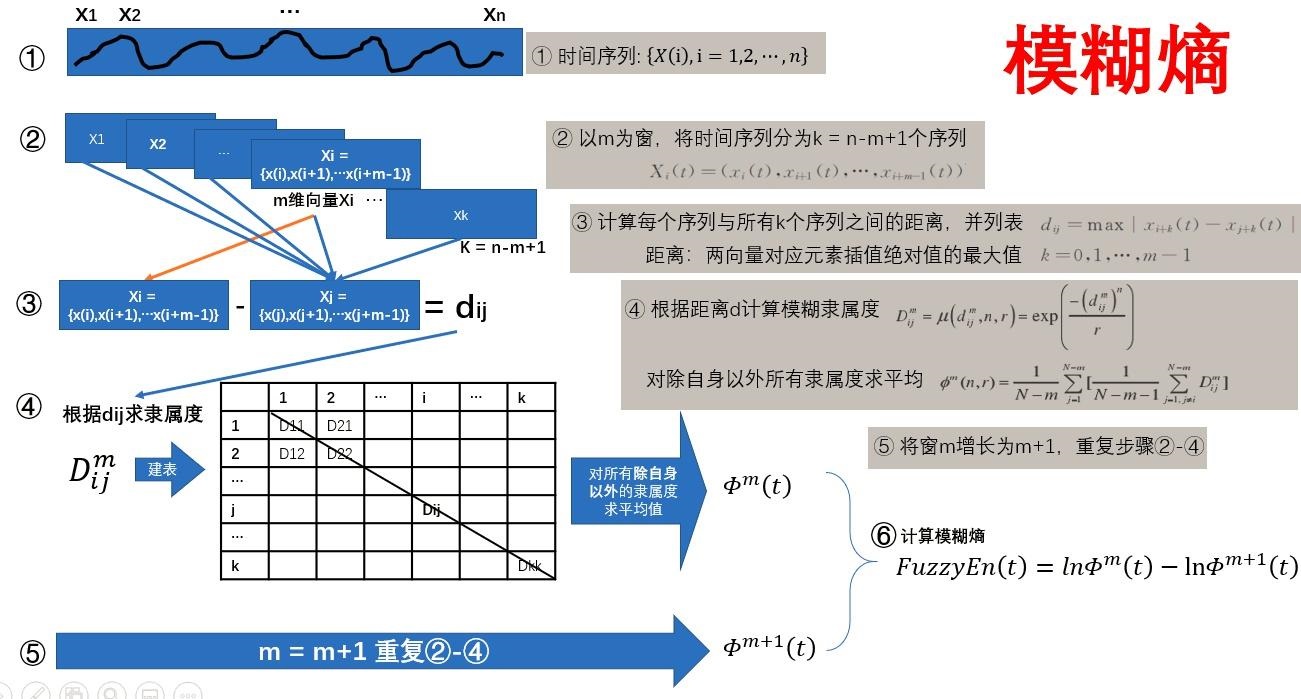
6、排列熵 (Permutation Entropy)
排列熵(Permutation Entropy, PE)是由Bandt和Pompe[7]提出的一种检测时间序列随机性和动力学突变行为的方法,具有计算简单、快速,抗噪能力强,适合在线监测等优点,已经被广泛应用于肌电信号和心率信号分析,气温复杂度以及机械故障检测等。
三、代码实现
以下为两个github代码仓库,提供了部分熵的python实现。
1、pyEntropy
nikdon/pyEntropy: Entropy for Python (github.com)
包括:
Shannon Entropy shannon_entropy
Sample Entropy sample_entropy
Multiscale Entropy multiscale_entropy
Composite Multiscale Entropy composite_multiscale_entropy
Permutation Entropy permutation_entropy
Multiscale Permutation Entropy multiscale_permutation_entropy
Weighted Permutation Entropy weighted_permutation_entropy
2、antropy
raphaelvallat/antropy: AntroPy: entropy and complexity of (EEG) time-series in Python (github.com)
import numpy as np
import antropy as ant
np.random.seed(1234567)
x = np.random.normal(size=3000)
# Permutation entropy
print(ant.perm_entropy(x, normalize=True))
# Spectral entropy
print(ant.spectral_entropy(x, sf=100, method='welch', normalize=True))
# Singular value decomposition entropy
print(ant.svd_entropy(x, normalize=True))
# Approximate entropy
print(ant.app_entropy(x))
# Sample entropy
print(ant.sample_entropy(x))
# Hjorth mobility and complexity
print(ant.hjorth_params(x))
# Number of zero-crossings
print(ant.num_zerocross(x))
# Lempel-Ziv complexity
print(ant.lziv_complexity('01111000011001', normalize=True))

