一、连续傅里叶变换
关于傅里叶变换的直观理解,大家可以移步B站UP主“3Blue1Brown”视频,这个视频讲解的很清楚。
傅里叶变换的公式为:
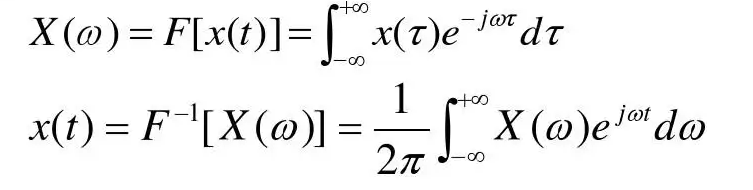
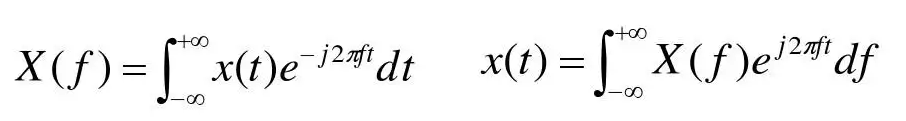
数字频率f与角频率ω之间的关系:
ω = f / fs * 2 * np.pi
其中fs为采样率
二、离散傅里叶变换
该部分后续补充
三、代码实现
# encoding:utf-8
"""
__time__ : 2022/4/10 17:10
__author__ : LIU SIYU
__email__ :18811379768@163.com
__address__ :Beijing Institute of Technology
"""
import numpy as np
from scipy.fftpack import fft, ifft
import matplotlib.pyplot as plt
from matplotlib.pylab import mpl
mpl.rcParams['font.sans-serif'] = ['SimHei'] # 显示中文
mpl.rcParams['axes.unicode_minus'] = False # 显示负号
# 采样点选择1400个,因为设置的信号频率分量最高为600赫兹,根据采样定理知采样频率要大于信号频率2倍,所以这里设置采样频率为1400赫兹(即一秒内有1400个采样点,一样意思的)
fs = 1400 # 信号采样率为fs,1400Hz
x = np.linspace(0, 1, fs)
# 设置需要采样的信号,频率分量有200,400和600
y = 7 * np.sin(2 * np.pi * 200 * x) + 5 * np.sin(2 * np.pi * 400 * x) + 3 * np.sin(2 * np.pi * 600 * x)
fft_y = fft(y) # 快速傅里叶变换
N = 1400
x = np.arange(N) # 频率个数
half_x = x[range(int(N / 2))] # 取一半区间
half_w = half_x / fs * (2 * np.pi)
abs_y = np.abs(fft_y) # 取复数的绝对值,即复数的模(双边频谱)
angle_y = np.angle(fft_y) # 取复数的角度
normalization_y = abs_y / N # 归一化处理(双边频谱)
normalization_half_y = normalization_y[range(int(N / 2))] # 由于对称性,只取一半区间(单边频谱)
plt.subplot(231)
plt.plot(x, y)
plt.title('原始波形')
plt.subplot(232)
plt.plot(x, fft_y, 'black')
plt.title('双边振幅谱(未求振幅绝对值)', fontsize=9, color='black')
plt.subplot(233)
plt.plot(x, abs_y, 'r')
plt.title('双边振幅谱(未归一化)', fontsize=9, color='red')
plt.subplot(234)
plt.plot(x, angle_y, 'violet')
plt.title('双边相位谱(未归一化)', fontsize=9, color='violet')
plt.subplot(235)
plt.plot(x, normalization_y, 'g')
plt.title('双边振幅谱(归一化)', fontsize=9, color='green')
plt.subplot(236)
plt.plot(half_w, normalization_half_y, 'blue')
plt.title('单边振幅谱(归一化)', fontsize=9, color='blue')
plt.show()

