PID控制算法及Python实现

项目开发

发布日期: 2022-05-04

更新日期: 2022-05-15

文章字数: 1.2k

阅读时长: 5 分

阅读次数:

PID控制算法及Python实现

1、PID算法简介

在控制领域，PID算法是应用最广泛的算法之一。
PID，就是“比例（proportional）、积分（integral）、微分（derivative）”，是一种很常见的控制算法。
常用于需要将某一个物理量“保持稳定”的场合（比如维持平衡，稳定温度、转速等）。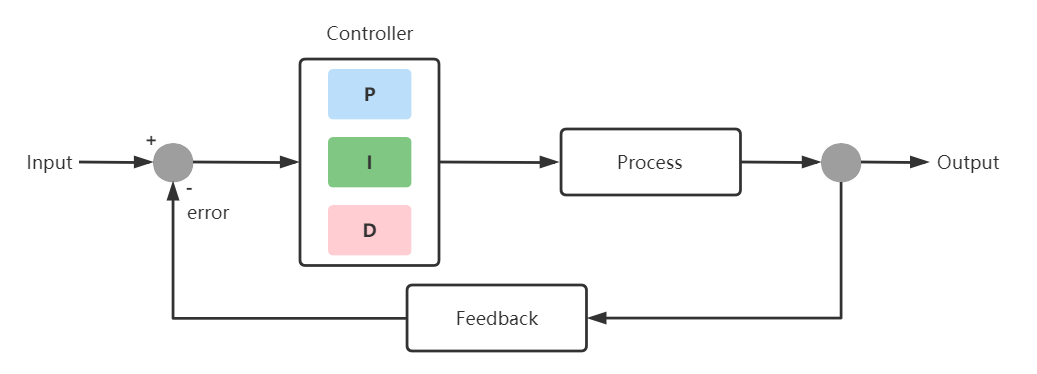
摘自网络

PID算法的公式为：
$\begin{array}{rcl} u (t) & = & K_{p} err (t) + K_{i} \int err (t) d t + K_{d} \frac{derr (t)}{d t} \end{array}$
对其进行离散化：
$\begin{matrix} u (n) = K_{p} err (n) + K_{i} \sum_{k = 0}^{n} err (k) + K_{d} (err (n) - err (n - 1)) \end{matrix}$

（1）P - 比例部分

比例环节的作用是对偏差瞬间作出反应。偏差一旦产生控制器立即产生控制作用，使控制量向减少偏差的方向变化。
控制作用的强弱取决于比例系数Kp，比例系数Kp越大，控制作用越强，则过渡过程越快，控制过程的静态偏差也就越小；
但是Kp越大，也越容易产生振荡，破坏系统的稳定性。
故而，比例系数Kp选择必须恰当，才能过渡时间少，静差小而又稳定的效果。

（2）I - 积分部分

从积分部分的数学表达式可以知道，只要存在偏差，则它的控制作用就不断的增加；
只有在偏差e(t)＝0时，它的积分才能是一个常数，控制作用才是一个不会增加的常数。
可见，积分部分可以消除系统的偏差。

（3）D - 微分部分

实际的控制系统除了希望消除静态误差外，还要求加快调节过程。
在偏差出现的瞬间，或在偏差变化的瞬间，不但要对偏差量做出立即响应（比例环节的作用），而且要根据偏差的变化趋势预先给出适当的纠正。为了实现这一作用，可在 PI 控制器的基础上加入微分环节，形成 PID 控制器。
我们需要一个控制作用，让被控制的物理量的“变化速度”趋于0，即类似于“阻尼”的作用。

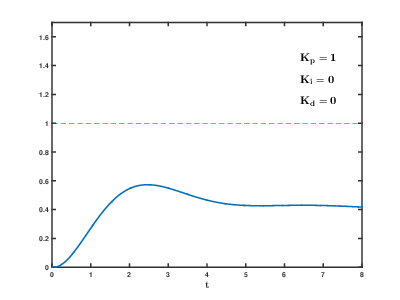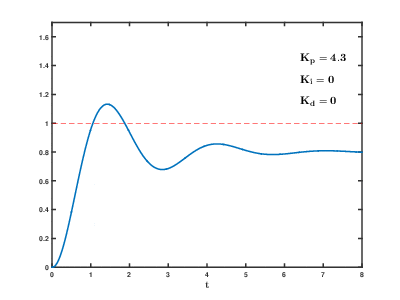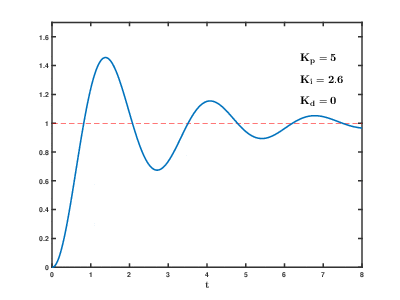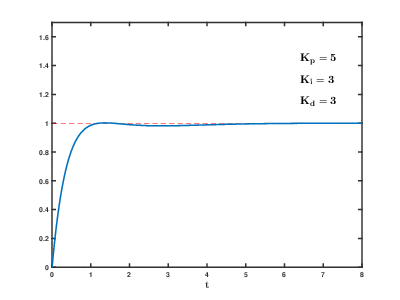
三个参数的作用（摘自网络）

2、PID算法原理

PID算法的原理详见下面UP主的视频：

3、Python实现

（1）位置式PID

位置式PID控制的输出与整个过去的状态有关，用到了误差的累加值。
位置式PID控制的累积误差相对更大。
位置式PID适用于执行机构不带积分部件的对象，如电液伺服阀。
位置式的输出直接对应对象的输出，因此对系统影响较大。

公式推导：
$\begin{matrix} Δ u = u (n) - u (n - 1) = K_{p} (err (n) - err (n - 1)) + K_{i} err (n) + K_{d} (err (n) - 2 err (n - 1) + err (n - 2)) \end{matrix}$

$\begin{matrix} u (n) = u (n - 1) + K_{p} (err (n) - err (n - 1)) + K_{i} err (n) + K_{d} (err (n) - 2 err (n - 1) + err (n - 2)) \end{matrix}$

（2）增量式PID

增量式PID的输出只与当前拍和前两拍的误差有关。
增量式PID控制输出的是控制量增量，并无积分作用，因此该方法适用于执行机构带积分部件的对象，如步进电机等。
由于增量式PID输出的是控制量增量，如果计算机出现故障，误动作影响较小，而执行机构本身有记忆功能，可仍保持原位，不会严重影响系统的工作

公式推导：
$\begin{matrix} u (n) = K_{p} e r r (n) + K_{i} \sum_{i = 0} e r r (i) + K_{d} [e r r (n) - e r r (n - 1)] \end{matrix}$

（3）代码实现

import time
import matplotlib.pyplot as plt
# from simple_pid import PID

# 解决中文显示问题
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False


class MyPID:
    def __init__(self, Kp=1.2, Ki=1., Kd=0.002):
        self.Kp = Kp  # 比例系数Proportional
        self.Ki = Ki  # 积分系数Integral
        self.Kd = Kd  # 微分系数Derivative

        self.Ek = 0  # 当前误差 e(k)
        self.Ek1 = 0  # 前一次误差 e(k - 1)
        self.Ek2 = 0  # 再前一次误差 e(k - 2)
        self.LocSum = 0  # 累计积分位置

    def PIDLoc(self, SetValue, ActualValue):
        '''
        PID位置(Location)计算
        :param SetValue:设置值(期望值)
        :param ActualValue:实际值(反馈值)
        :return:PID位置
        '''
        self.Ek = SetValue - ActualValue
        self.LocSum += self.Ek  # 累计误差

        PIDLoc = self.Kp * self.Ek + (self.Ki * self.LocSum) + self.Kd * (self.Ek1 - self.Ek)

        self.Ek2 = self.Ek1
        self.Ek1 = self.Ek

        return PIDLoc

    def PIDInc(self, SetValue, ActualValue):
        '''
         PID增量(Increment)计算
        :param SetValue: 设置值(期望值)
        :param ActualValue:实际值(反馈值)
        :return: 本次PID增量(+/-)
        '''
        self.Ek = SetValue - ActualValue
        PIDInc = (self.Kp * self.Ek) - (self.Ki * self.Ek1) + (self.Kd * self.Ek2)

        self.Ek2 = self.Ek1
        self.Ek1 = self.Ek
        return PIDInc

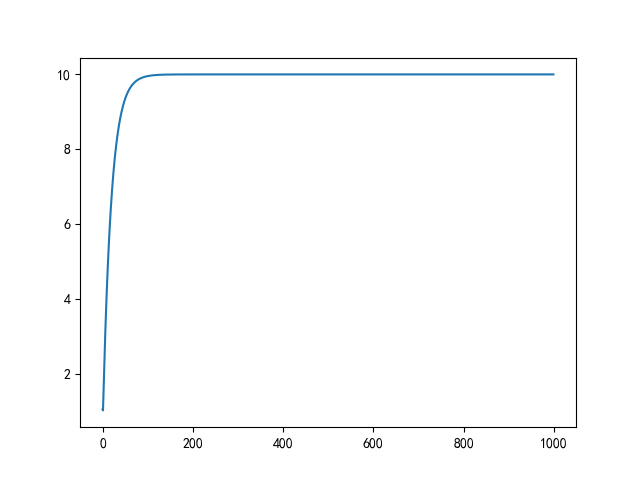
# 位置式
myPID = MyPID(Kp=0.9, Ki=0.15, Kd=0.7)
SetValue = 10
ActualValue = 1
ActualValue_list = []
for i in range(1000):
    PIDLoc = myPID.PIDLoc(SetValue, ActualValue)
    ActualValue = PIDLoc
    print(ActualValue)
    ActualValue_list.append(ActualValue)

plt.plot(ActualValue_list)
plt.show()

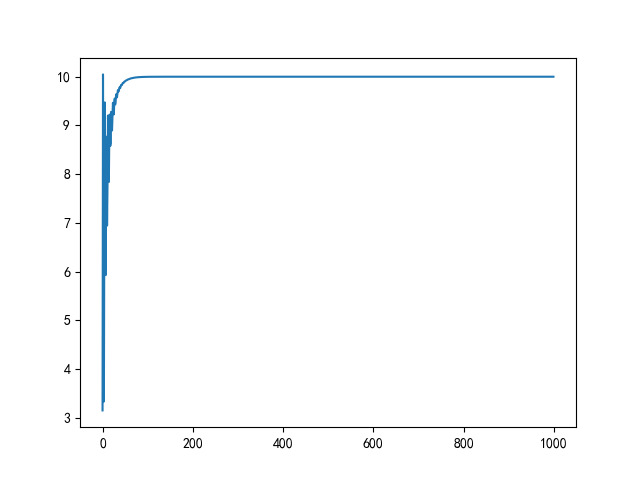
# 增量式
myPID = MyPID(Kp=0.005, Ki=0.008, Kd=0.05)
SetValue = 10
ActualValue = 1
ActualValue_list = []
for i in range(1000):
    PIDInc = myPID.PIDInc(SetValue, ActualValue)
    ActualValue += PIDInc
    print(ActualValue)
    ActualValue_list.append(ActualValue)

plt.plot(ActualValue_list)
plt.show()