基于稳态视觉诱发电位的BCI系统是目前最常用的头皮脑电BCI系统之一,该系统以稳态视觉诱发电位(Steady-state visual evoked potentials, SSVEP)作为目标信号。SSVEP是一种通过向受试者呈现以一定频率快速闪烁的刺激块,在头皮上记录到的与刺激频率倍频相同的稳态脑电响应。
下图展示了给某位受试呈现了以12Hz闪烁的刺激块时受试者脑电的频域和时域特性。在频域中,我们可以清楚地观察到在12,24,36和48Hz,也就是刺激频率的1倍频,2倍频,3倍频和4倍频处有明显的峰值,而在时域上也可以看到稳定的周期响应。

SSVEP BCI进行目标识别的原理简单地来说就是检测脑电信号中是否存在某些特定的频率成分。2002年,清华大学团队设计了一个控制光标二维移动的BCI系统,4个闪烁块按照不同频率闪烁,每个闪烁块编码不同的命令(上下左右),当用户希望控制光标向上,只需要注视对应的闪烁块(假设闪烁频率为12Hz),从而诱发对应频率的SSVEP信号,如果系统检测到12Hz的SSVEP响应,则判断用户在注视向上的光标,从而给出反馈。
几种典型算法
由于SSVEP具有显著的频域特征,在早年的SSVEP-BCI研究中,多采用基于功率谱方法(PSD)对信号进行检测,以下述参考文献为例,研究者对采集到的脑电数据进行频谱分析,通过提取频域能量峰值所在的频率点来对目标进行识别。但这种方法易受噪声干扰,性能有限,近年来越来越多的研究者将SSVEP的时域信息纳入到了分析中来。
参考文献
Ming Cheng, Xiaorong Gao, Shangkai Gao, Dingfeng Xu,Design and Implementation of a Brain-Computer Interface with High Transfer Rates. IEEE Transaction on Biomedical Engineering,VOL. 49, NO. 10, p1181-1186, 2002
CCA(典型相关分析)
CCA是一种度量两组信号之间线性相关性的多元统计方法,在SSVEP-BCI中取得了广泛的应用。
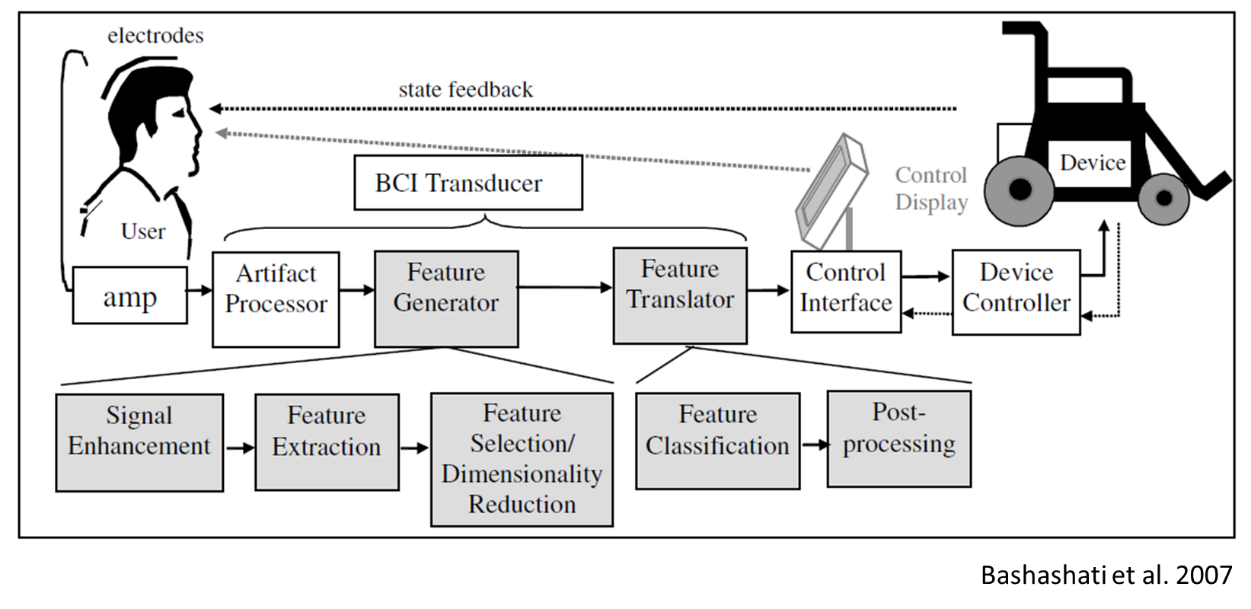
CCA的目标是找到两个线性组合WX和WY,使得原有的多通道信号x1,x2,…,xn和y1,y2,…,yn相关系数最大。在实际应用时,x1,x2,…,xn为多通道的脑电信号,y1,y2,…,yn为参考信号,即刺激频率的倍频对应的正余弦波。对一段待分类的脑电数据来说,可以计算其与多个参考信号的典型相关系数,比较这些典型相关系数的大小,得到最大相关系数的参考信号对应的频率即为刺激频率。
参考文献
Bin G, Gao X, Yan Z, Hong B, Gao S: An online multi-channel SSVEP-based brain-computer interface using a canonical correlation analysis method. J Neural Eng; 2009 Aug;6(4):046002
Template-based CCA
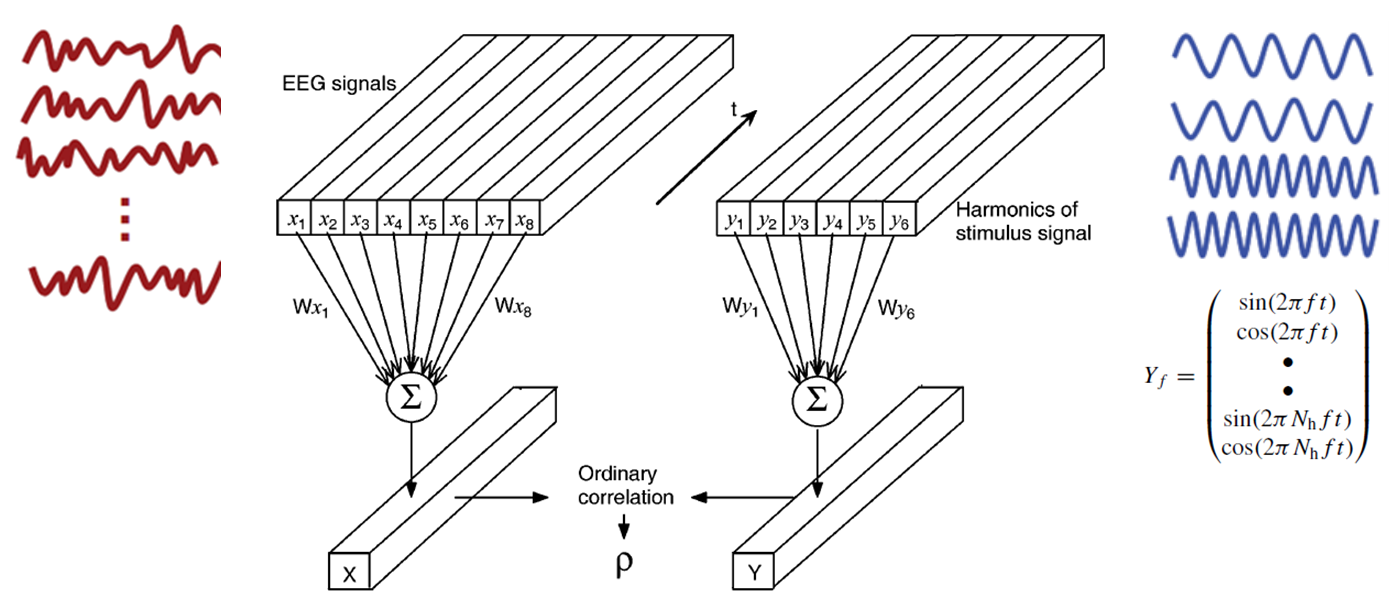
上面所述的CCA方法采用正余弦信号作为参考信号,并未充分利用脑电本身的信息,于是出现了Template-based CCA 这一方法,它的基本思想和计算流程和传统CCA方法完全一样,差异在于,Template-based CCA 将之前记录的,已知刺激频率的脑电数据的叠平均信号作为模板,来估计空域滤波器,相较于传统CCA,叠平均得到的模板和空域滤波器可以更好的反映受试者的脑电特异性,因此具有更好的性能。
参考文献
Bin, G., Gao, X., Wang, Y., Li, Y., Hong, B., & Gao, S. (2011). A high-speed BCI based on code modulation VEP. Journal of Neural Engineering, 8(2).
Filter-bank CCA
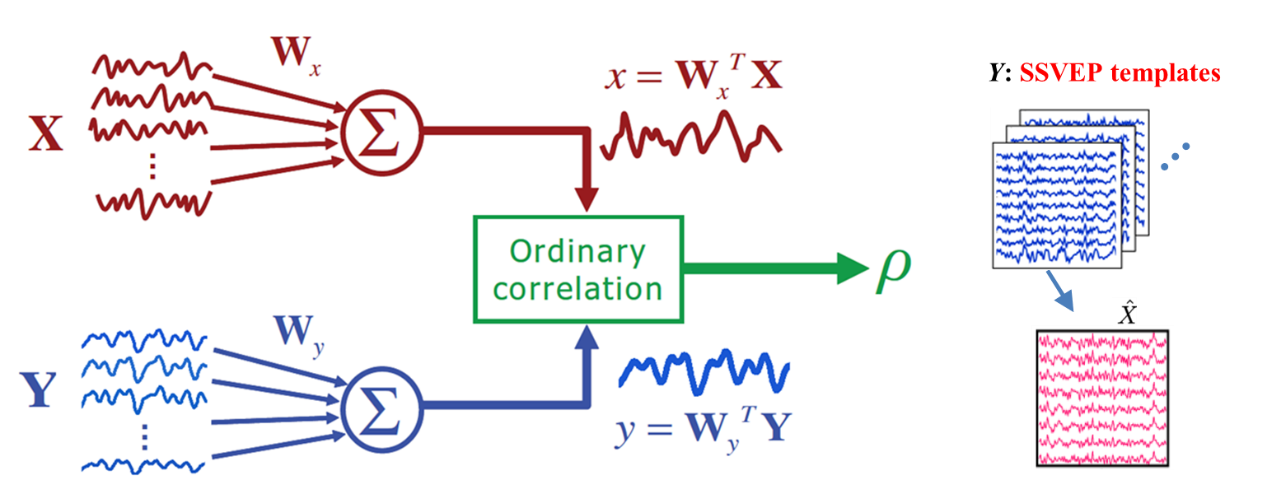
为了有效地利用SSVEP的基频和谐波信息,从而进一步提高识别精度,下述参考文献提出了基于滤波器组的典型相关分析方法(filter-bank CCA)。
该方法分为三步,首先是进行滤波器组分析,简单地说即是将脑电数据滤波到不同子带;然后是对每一个子带的数据做CCA得到典型相关系数;最后,通过将各个频带数据的典型相关系数进行加权求和,取和不同参考信号得到的加权和的最大值对应的频率为识别目标。
参考文献
Chen, X., Wang, Y., Gao, S., Jung, T., & Gao, X. (2015). Filter bank canonical correlation analysis for implementing a high-speed SSVEP-based brain–computer interface. Journal of Neural Engineering, 12(4).
任务相关成分分析(Task-related Component Analysis, TRCA)
TRCA的主要思想是寻找一个线性组合,使得原始数据中与事件相关的频率成分在多次试验的可重复性最大,该方法在SSVEP目标识别中取得了很好的效果。
TRCA方法的具体实现方法如下。首先假设存在两种源信号:1)任务相关信号s(t); 2)任务无关信号 n(t)。因此,检测到的多通道EEG信号的线性模式可以表述为:
, j = 1, 2, … , (3-1)
其中,j是通道编号,和是将原信号投影到EEG信号的系数。需要解决的问题是如何从观察信号的线性组合中恢复出任务相关信号。的线性组合可以表示为:
(3-2)
我们可以通过最大化试次之间协方差的方式求解这个问题。假设第h个试次的EEG信号和预测的任务相关成分分别为和,h = 1,2, … ,。对应的时间范围是。这里,是每个任务试次的长度。而第和个试次之间的协方差可以被写作:
(3-3)
各个试次之间可能的组合可以表示为:
(3-4)
其中,矩阵可以被写作:
(3-5)
为了得到有限个解,的方差被限制为:
(3-5)
因此,我们可以把求解转化成以下问题:
(3-7)
其中,可以通过求解矩阵特征值的方式获得。
参考文献
Nakanishi, M., Wang, Y., Chen, X., Wang, Y., Gao, X., & Jung, T. (2018). Enhancing Detection of SSVEPs for a High-Speed Brain Speller Using Task-Related Component Analysis. IEEE Transactions on Biomedical Engineering, 65(1), 104-112.
备注
本文章为公益性质,旨在为脑机接口开发人员、研究人员提供数据下载途径,共同促进脑机接口行业的发展。
如有侵权,请联系博主。
若诉求合理,可删除文章。
如链接失效,可联系博主微信:BCIRobot


